Mathematical Prologue: Scenes 3 – 8 focus on geometric optics to establish a success story for modeling. The models are based on three mathematical principles which can be dealt with at various mathematical levels. The three principles are:
- Fermat’s Principle: In its simplest and most anthropomorphic form Fermat’s Principle states that light traveling from one point to another follows the fastest path. This form is sufficient for much of the work we do here. The more sophisticated and useful form is that light follows a path that is a critical point of the time traveled function. In a Calculus or post-Calculus course this form should be introduced.
- Snell’s Law: Snell’s Law provides a relationship between the angle of incidence and angle of coincidence of light crossing a boundary between two mediums in which it travels at different speeds. The derivation of Snell’s Law from Fermat’s Principle is a standard Calculus problem. See the problem below from Stewart’s Calculus book. Note that the angles are measured with respect to the normal vector to the boundary at the point where the light crosses. This is particularly convenient for us because we will look at planar and spherical boundaries and the normal vector is easily found without using Calculus.
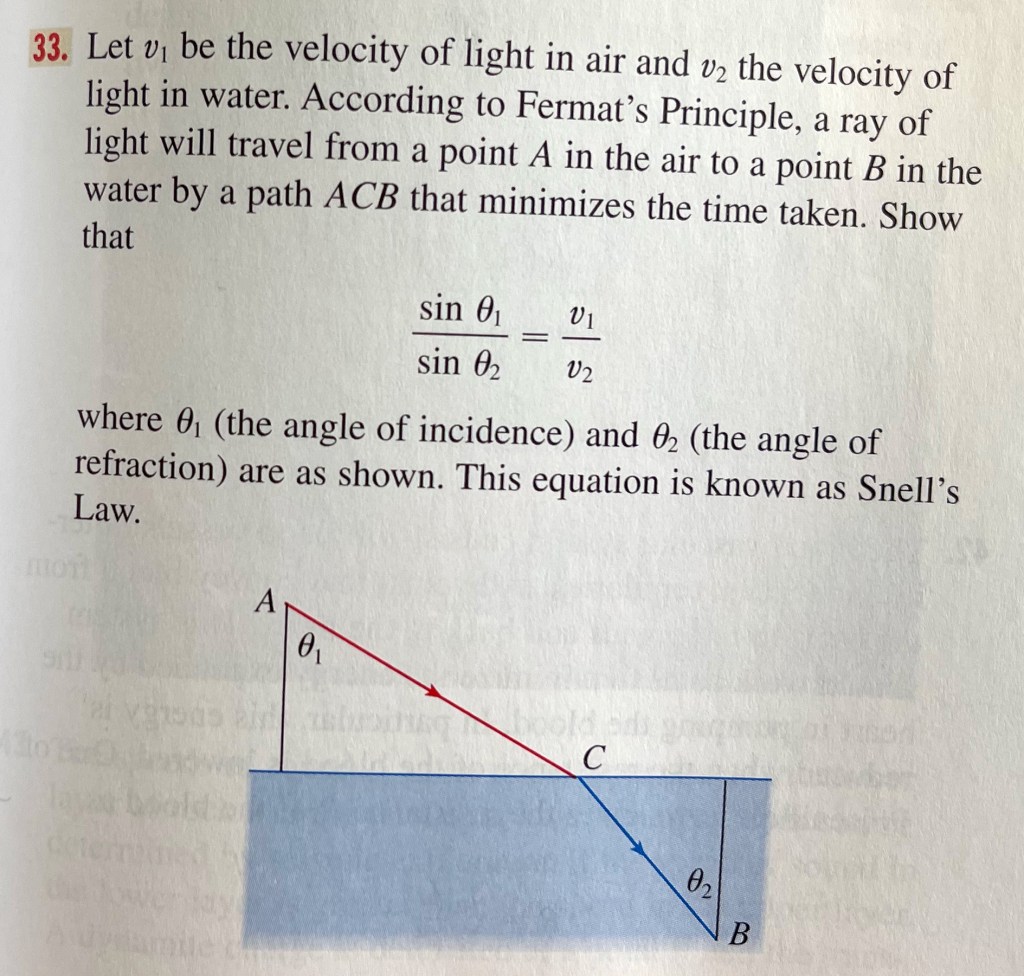
- The Law of Reflection: The Law of Reflection states that when light bounces off a reflective surface then the angles of incidence and coincidence are equal. This law is easily derived from Fermat’s Law for a flat surface using elementary geometry (See This) and for a more general surface using Calculus.
Students should know a bit about two- and three-dimensional vectors and can be either pre-Calculus, taking Calculus or post-Calculus.
ACTORS: You are playing the part of your students who are living the lives of scientists building an understanding of light and optics. The material in these scenes can enrich and motivate single and multivariable Calculus courses.
This is a prelude and background for later study of quantum science.
In your role you have very limited knowledge of light and optics. Basically, we begin with the RGB model of color and are limited to the observations and experiments we do in this act. Please stay in your role.
- Scene 1: Color based on the RGB Model
- Scene 2: Polarization
- Scene 3: Geometric Optics – The Mirascope
- Scene 4: Geometric Optics -Refraction and Fishing
- Scene 5: Geometric Optics – Refraction As Seen By A Fish
- Scene 6: Geometric Optics – Refraction – Crystal Balls
- Scenes 7 and 8 look at reflection in curved mirrors. Here is a short unit that uses just elementary geometry to study reflections in flat mirrors.
- Scene 7: Geometric Optics – Reflection and Make-up Mirrors
- Scene 8: Geometric Optics – Reflection and Traffic
- Scene 9: Geometric Optics Breaks Down – Diffraction
Big Open Questions
We’ve come a long way. We’ve been able to build models that work for many different optical phenomena. We’ve looked at some of the evidence for wave mechanics and we’ve seen many different phenomena both ones for which we have good models and ones for which we have many questions. We’ve set the stage for studying quantum science. One nice introduction is this talk from Qiskit. In particular, it discusses three difficult but essential ideas in quantum science and quantum computing.
- Superposition: We usually think of something as being one state or another but superposition allows something to be in a probabilistic combination of several states at once. This idea is very unsettling for those of us who live in a world whose scale is larger than the quantum scale. In fact, Einstein famously said, “God does not play dice … “
- Entanglement: The possibility that states of two different particles in two different places are connected.
- Interference
There is a wealth of experimental evidence supporting these ideas, however strange they seem to be at first. We can’t reach an understanding of these ideas in a short minicourse like this whether we’re mathematicians or our students but we hope that we’ve laid a basis for further work.