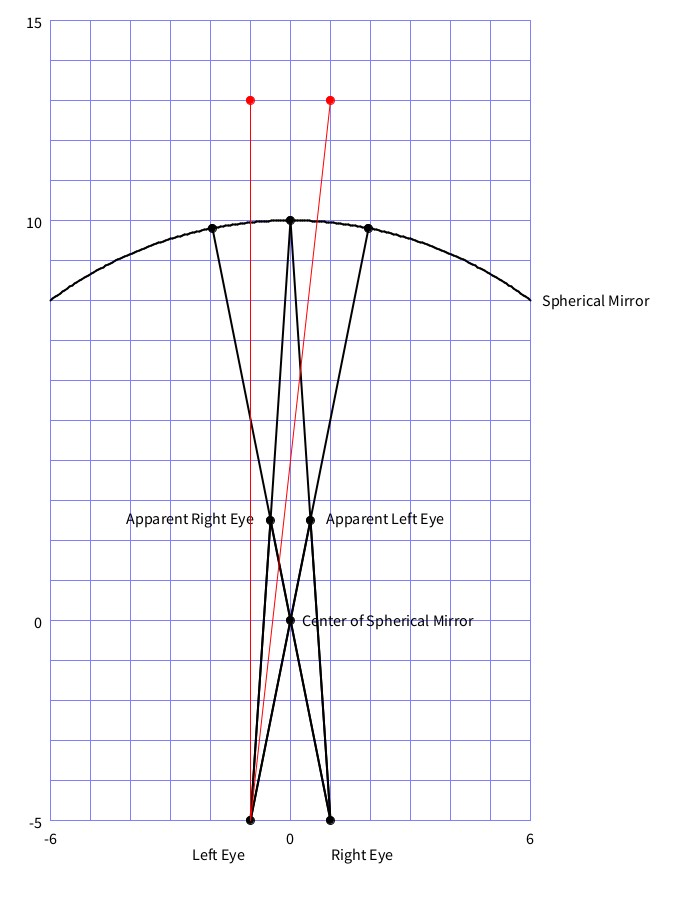
The first problem can be solved without any algebra or technology and just a bit of geometry. See the figure above. We begin by finding four paths:
- The path followed by light traveling from the left eye (as a target) to the mirror and then back to the left eye (now as an eye).
- The path followed by light traveling from the left eye (as a target) to the mirror and then to the right eye (as an eye).
- The path followed by light traveling from the right eye (as a target) to the mirror and then to the left eye (as an eye).
- The path followed by light traveling from the right eye (as a target) to the mirror and then back to the right eye (now as an eye).
For the first path (left eye to mirror and then back to left eye), look at the line that starts at the center of the mirror and goes to the left eye (this part of the line is red) and then continues in black to the mirror where is hits the mirror at a right angle and bounces back to the left eye. This black segment of the line, first from eye to mirror and then from mirror back to eye, is this first path. The left eye thinks it is on the apparent path that extends this line beyond the mirror. We can analyze the fourth path (right eye to mirror and back to right eye) in the same way.
To analyze the middle two paths (from left eye as target to right eye as eye or vice versa). Look at the two line segments from each eye to the point (0, 10). These two segments comprise the two lines. The path from the left eye as target goes first from that eye to the point (0, 10) and then from the point (0, 10) to the right eye as eye. Notice the tangent to the mirror at the point (0, 10) is horizontal.
Finally, we find the apparent position of the two eyes by looking at the intersections of the appropriate apparent paths.
Notice that the apparent position of the two eyes is about eleven inches from the eyes and the mirror is only three inches from the eyes. So your eyes are able to focus on their apparent images even though your eyes are so close to the mirror.
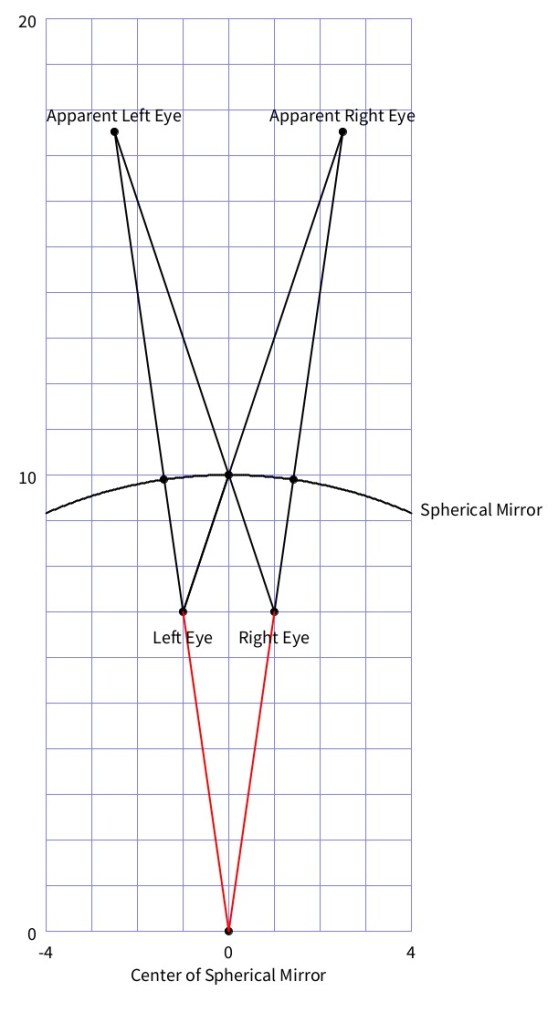
The figure below can help you analyze what you see in a make-up mirror from further away.