Your house and your students’ houses are great places to learn mathematics and use it to understand and discover some surprising and powerful optical phenomena. They are well-equipped optical laboratories. For example, you can experiment with refraction in any washbasin. Use your mouse to drag the vertical bar back-and-forth in the figure below to see how refraction changes the apparent position of the drain in the bottom of the washbasin.


This is the first of a series of modeling scenes (Act I, Scenes 4-8) that develop the power of geometric optics to predict, explain and verify experimentally. Each scene tells a story using a model to make an often unexpected prediction and then testing that prediction with a simple experiment. You and your students will need a way to minimize a function and some simple “equipment” from around the house or indoor SWAG.
Our first model, for color, was based on a simple, even overly simple, model of color – the RGB model. Now we use a simple model for how light travels. This is a simple version “light follows the fastest path” from one point (a target) to another (an eye)” of Fermat’s principle. The figure below is used to understand phenomena refraction in a washbasin using this principle.
Light travels at a speed of 30 cm/ns in air and 22.5 cm/ns in water. The mathematical skill anthropomorphic photons need is finding the minimum of a function. You and your students may use Calculus or technology like graphing calculators or Desmos. The figure below shows a typical problem,
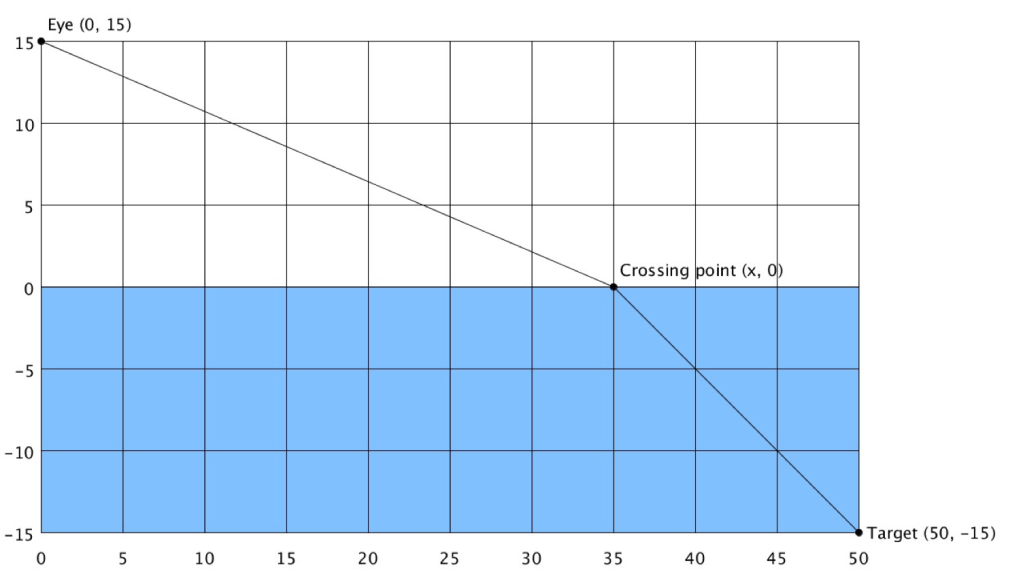
which can be solved by minimizing the function:
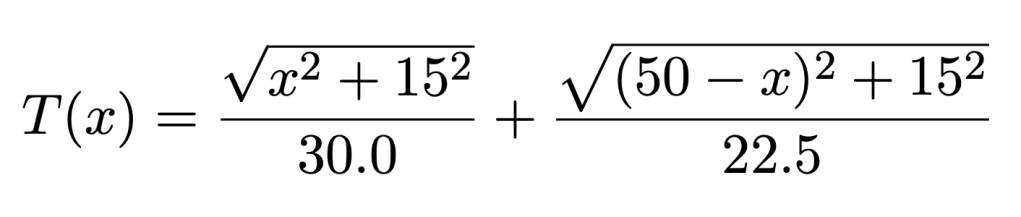
for 0 <= x <= 50.
Use these ideas to determine the apparent position of a fish that is underwater as seen by a fisherman whose eyes are above the water. Verify your method using a washbasin.
For instructors only after you have completed the scene click on SPOILER ALERT.